Tag Archives: binomial coefficient

03/10/2016 · 9:37 pm

A Combinatorial Identity

While tutoring today a student asked me about the following identity

$(*)\qquad\qquad\qquad\displaystyle\sum_{n\ge i\ge j\ge k\ge 0}\binom ni\binom ij\binom jk=4^n$ .

One way to prove it is to count the number of possible triples $(A,B,C)$ of sets with $C\subseteq B\subseteq A\subseteq S=\{1,\dots,n\}$ . This can be done in two ways. First, if $A, B, C$ contain $i,j,k$ elements respectively then the number of such triples clearly equals the left-hand side of $(*)$ . On the other hand, since each element of $S$ must belong to one of the four disjoint regions in the picture below

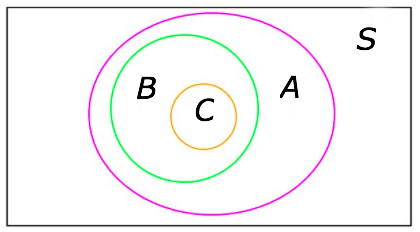
screenshot-2016-10-03-21

the number of such triples equals precisely $4^n$ .

An algebraic proof can be obtained by repeated use of the binomial theorem:

$\displaystyle 4^n=\sum_{n\ge i\ge 0}\binom ni3^i=\sum_{n\ge i\ge j\ge 0}\binom ni\binom ij2^j=\sum_{n\ge i\ge j\ge k\ge 0}\binom ni\binom ij\binom jk$ .

Similarly, one obtains the more general identity

$\displaystyle\sum_{n\ge i_m\ge\cdots\ge i_1\ge 0}\binom{n}{i_1}\binom{i_1}{i_2}\cdots\binom{i_{m-1}}{i_m}=(m+1)^n$ .

This also follows from the multinomial theorem since the left-hand side equals

$\displaystyle\sum_{n\ge i_m\ge\cdots\ge i_1\ge 0}\frac{n!}{(n-i_1)!(i_1-i_2)!\cdots (i_{m-1}-i_m)!i_m!}=(m+1)^n$ .

Leave a comment

Filed under Combinatorics

Tagged as binomial coefficient, partition

17/10/2015 · 1:57 pm

Products of Consecutive Integers Dividing One Another

I’ve been working on a project lately and I find myself stuck with the following problem.

Problem. Given positive integers $a<b$ , what can be said about the least positive integer $t$ such that $a(a+1)\cdots (a+t)$ does not divide $b(b-1)\cdots (b-t)$ ?

Obviously $t$ is bounded above by $b-a+1$ but this is very weak. Probably the least $t$ should be close to $b/a$ .

Leave a comment

Filed under Number Theory

Tagged as binomial coefficient

02/10/2015 · 8:50 pm

A Nice Divisibility Result on Binomial Coefficients

I just came across this cute little result on Quora and generalised it to the following.

Proposition. For any integers $0\le k\le n$ ,

$\displaystyle\frac{n}{(n,k)}$ divides $\displaystyle\binom{n}{k}$ .

First proof. Note that

$\displaystyle \frac{k}{(n,k)}\binom nk=\frac{n}{(n,k)}\binom{n-1}{k-1}$ .

Since $\displaystyle\left(\frac{n}{(n,k)},\frac{k}{(n,k)}\right)=1$ , the result follows. $\square$

Second proof. Let $n=p_1^{a_1}\cdots p_r^{a_r}$ and $k=p_1^{b_1}\cdots p_r^{b_r}$ where $p_1,\dots,p_r$ are the prime factors of $nk$ . For each $i$ , the base $p_i$ representations of $n$ and $k$ have $a_i$ and $b_i$ trailing zeros respectively. Hence $p_i^{\max\{a_i-b_i,0\}}$ divides $\displaystyle\binom nk$ , by Kummer’s theorem. Therefore

$\displaystyle k\prod_{i=1}^rp_i^{\max\{a_i-b_i,0\}}=\prod_{i=1}^rp_i^{\max\{a_i,b_i\}}=[n,k]$

divides $\displaystyle k\binom nk$ . Now the result follows using $[n,k]/k=n/(n,k)$ . $\square$

A nice corollary is the following property of Pascal’s triangle.

Corollary. For any integers $0<k<n$ ,

$\displaystyle\gcd\left(n,\binom nk\right)>1$ .

Using the identity

$\displaystyle\binom nk\binom kr=\binom nr\binom{n-r}{k-r}$

the argument in the first proof above can be adapted to prove the following generalisation:

Proposition. For any integers $0\le r\le k\le n$ ,

$\displaystyle\frac{\binom nr}{\left(\binom nr,\binom kr\right)}$ divides $\displaystyle\binom{n}{k}$ .

Corollary. Any two entries $\neq 1$ in a given row of Pascal’s triangle have a common factor $>1$ .

Leave a comment

Filed under Number Theory

Tagged as binomial coefficient, prime power

08/04/2015 · 2:15 am

Binomial Sum Modulo Prime Power: Part 2

Let $p$ be a prime number and $\omega=\exp(2\pi i/p)$ . Recall that we conjectured in this post that

$(*)\qquad\qquad\qquad\displaystyle\sum_{j=0}^{p-1}(1-\omega^j)^n=p\sum_{k=0}^{\lfloor n/p\rfloor}(-1)^{kp}\binom{n}{kp}$

is divisible by $p^{\lceil n/(p-1)\rceil}$ . From exercise 2 of this post we know that $(p)$ factors as $(p,\omega-1)^{p-1}$ into prime ideals in the ring $\mathbb Z[\omega]$ . So $(\omega-1)^{p-1}\in (p)$ . Therefore the right-hand side of $(*)$ is divisible by $p^{\lfloor n/(p-1)\rfloor}$ . So we are off by at most one factor of $p$ ! I believe this approach can be improved upon to account for the extra factor, since we haven’t used any property of the sum.

Furthermore,

$\displaystyle\sum_{j=0}^{p-1}\omega^{-rj}(1-\omega^j)^n=p\sum_{m\equiv r\pmod p}(-1)^m\binom{n}{m}$

for any $r$ . So our best result thus far is the following:

Theorem (weaker version of Fleck’s).

$\displaystyle\sum_{m\equiv r\pmod p}(-1)^m\binom{n}{m}\equiv 0\pmod{p^{\lfloor\frac{n}{p-1}\rfloor-1}}$ .

Goal: Improve the floors to ceilings.

Leave a comment

Filed under Algebra, Number Theory

Tagged as binomial coefficient, ideal, prime power, root of unity

28/03/2015 · 1:31 pm

Binomial Sum Modulo Prime Power: Part 1

In the last post we showed that

$\displaystyle N_p(n)\equiv\sum_{k=1}^{\lfloor n/p\rfloor}(-1)^k\binom{n}{pk}\pmod p$

and then we used Lucas’ theorem to evaluate the sum modulo $p$ .

My initial attempt at evaluating the sum was to note that

$(*)\qquad\qquad\qquad\displaystyle\sum_{j=0}^{p-1}(1-\omega^j)^n=p\sum_{k=0}^{\lfloor n/p\rfloor}(-1)^{kp}\binom{n}{kp}$

where $\omega=\exp(2\pi i/p)$ , but then I was stuck. Numerical examples suggested that this sum is in fact divisible by $p^{\lceil n/(p-1)\rceil}$ , but I could not think of a way of extending the argument from the last post. Nonetheless, some extensive google search recently revealed that

Theorem (Fleck, 1913). For any $j$ ,