This idea first came to my mind a long time ago when I was trying to generalise the application of the division algorithm. All I came up with is the following:
Proposition 0. Let  be a subgroup of
be a subgroup of  . If
. If  has a least positive element, then
has a least positive element, then  is cyclic. Otherwise
is cyclic. Otherwise  has arbitrarily small positive elements.
has arbitrarily small positive elements.
A few days ago, in a Number Theory lecture, we proved that the minimal solution to Pell’s equation generates all solutions. It reminded me of the division algorithm again, so it was time again to try to generalise this, because now I have a few more tools in hand!
Let’s say  is a set where the division algorithm applies. We definitely need some sort of partial order in
is a set where the division algorithm applies. We definitely need some sort of partial order in  to say that the ‘remainder’ must be ‘less than’ the ‘divisor’. We might want
to say that the ‘remainder’ must be ‘less than’ the ‘divisor’. We might want  to be closed under some operation (so that we can repeatedly ‘subtract’ the ‘divisor’ from the ‘dividend’) and we also need an inverse operation (i.e. the ‘subtraction’).
to be closed under some operation (so that we can repeatedly ‘subtract’ the ‘divisor’ from the ‘dividend’) and we also need an inverse operation (i.e. the ‘subtraction’).
So first of all, we need  to be a poset. In addition, the closure and inverse operations suggest that we want
to be a poset. In addition, the closure and inverse operations suggest that we want  to be a group. How should the order behave under the group operation? Clearly we want it to be compatible with the operation. We also probably want the inverse of a ‘positive’ element to be ‘negative’, and vice-versa. Do we need the group to be abelian? Maybe, but let’s not impose that condition yet.
to be a group. How should the order behave under the group operation? Clearly we want it to be compatible with the operation. We also probably want the inverse of a ‘positive’ element to be ‘negative’, and vice-versa. Do we need the group to be abelian? Maybe, but let’s not impose that condition yet.
So to put our ideas into work, let 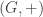 be a group with a partial order
be a group with a partial order 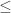 such that for all
such that for all 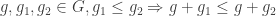 and
and 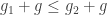 . We say that an element
. We say that an element 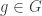 is positive if
is positive if  , where
, where  is the identity element of
is the identity element of  . Define the positive cone of
. Define the positive cone of  to be the set
to be the set  of all positive elements.
of all positive elements.
Okay now we hopefully have all the necessary definitions in place. Let’s see if we can prove anything using these. The first thing that we want is probably: if  , then
, then  . This follows easily:
. This follows easily:  , add
, add 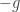 to both sides and we are done. It works the other way around as well, so in fact we have proved:
to both sides and we are done. It works the other way around as well, so in fact we have proved:
Lemma 1.  .
.
That was good. We wanted the inverse of positive elements to be negative and it just followed from the definition. But we want more! So take a non-zero element 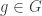 . By Lemma 1 we can take
. By Lemma 1 we can take  to be positive without loss of generality. How about adding something to both sides of
to be positive without loss of generality. How about adding something to both sides of  again? Last time we added
again? Last time we added 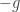 . We can add
. We can add  , but that doesn’t change anything. So the only obvious choice left is to add
, but that doesn’t change anything. So the only obvious choice left is to add  :
:  . Now what? Let’s add
. Now what? Let’s add  again!
again!  , i.e.
, i.e.  . Combining the last two gives
. Combining the last two gives  . It follows by induction that
. It follows by induction that  for all integers
for all integers 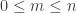 (note: here
(note: here  ,
,  times). This looks promising.
times). This looks promising.
What about ‘negative’ elements? Note that by Lemma 1,  . Adding
. Adding 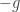 to both sides yields
to both sides yields  , and so on. So we have another nice result:
, and so on. So we have another nice result:
Lemma 2.  for all integers
for all integers 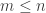 and
and 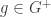 .
.
It seems that this is all we can derive from our first principles. So let’s apply more restrictions on  . Let
. Let 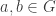 be positive with
be positive with  . As in the division algorithm, let’s look at
. As in the division algorithm, let’s look at 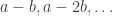 etc. We want this sequence to stop as soon as
etc. We want this sequence to stop as soon as  becomes negative. How do we do this? In other words, we want the set
becomes negative. How do we do this? In other words, we want the set  to have a least positive element. Did something just pop up in your mind? A set having a least element must have reminded you of something like… the well-ordering principle! So how about we impose the extra condition that
to have a least positive element. Did something just pop up in your mind? A set having a least element must have reminded you of something like… the well-ordering principle! So how about we impose the extra condition that 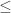 is a well-order on
is a well-order on  ? Well, that’s clearly absurd, because for any positive
? Well, that’s clearly absurd, because for any positive  the set
the set 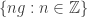 has no least element. How about least positive element then? In other words, let’s say
has no least element. How about least positive element then? In other words, let’s say  is well-ordered under
is well-ordered under 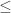 .
.
Now  has quite a few nice properties: it is a group under
has quite a few nice properties: it is a group under  ,
, 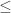 is an order on
is an order on  preserving
preserving  , and its positive cone is well-ordered. Let’s see if our ideas work now.
, and its positive cone is well-ordered. Let’s see if our ideas work now.
Let  be the least non-zero element in
be the least non-zero element in  and
and 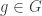 be any non-zero element. Without loss of generality,
be any non-zero element. Without loss of generality, 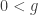 . Then
. Then 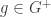 so
so  . Consider the elements
. Consider the elements  for
for  . We want
. We want 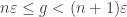 for some
for some  . Can we achieve this? We certainly have
. Can we achieve this? We certainly have  for
for 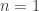 , so we need
, so we need  for some
for some  . By Lemma 2
. By Lemma 2  must be greater than
must be greater than  . How do we know that
. How do we know that  exists?
exists?
Suppose it doesn’t. Then  for all
for all  by totality (recall that a well-order is a total order) and Lemma 2. Then
by totality (recall that a well-order is a total order) and Lemma 2. Then  , so
, so  . Hence
. Hence  , so it has a least element
, so it has a least element 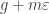 . Then
. Then  which implies
which implies  for all
for all  , a contradiction.
, a contradiction.
That was really good! Now we can take the maximal  such that
such that  . Then
. Then  . Then
. Then  ; the left inequality says
; the left inequality says 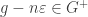 , and the right inequality says
, and the right inequality says  . So
. So 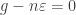 and
and  . This is exactly what we wanted.
. This is exactly what we wanted.
We have shown that  . In fact we can do more. Clearly
. In fact we can do more. Clearly  cannot be finite. Because otherwise
cannot be finite. Because otherwise  must have finite order, i.e.
must have finite order, i.e.  for some positive integer
for some positive integer  . Then
. Then  by Lemma 2. So all of these must be equalities (by antisymmetry), i.e.
by Lemma 2. So all of these must be equalities (by antisymmetry), i.e.  , a contradiction.
, a contradiction.
So our restrictions have not only worked, we’ve shown that all groups with these properties essentially have the same structure, that of the infinite cyclic group. Let’s give  a name: we say that the group
a name: we say that the group  is well-ordered if the set
is well-ordered if the set  is well-ordered under
is well-ordered under 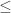 . We have thus proved:
. We have thus proved:
Proposition 1. The only non-trivial well-ordered group is the group  of integers (up to isomorphism).
of integers (up to isomorphism).
Now we can give one-line proofs of the following facts using our Proposition 1: (here any ordering is under the usual  order in
order in 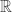 )
)
Corollary 1. The 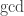 of two natural numbers exists, and is their least positive linear combination.
of two natural numbers exists, and is their least positive linear combination.
Proof. For  , the additive group
, the additive group 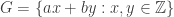 is well-ordered, and so is equal to
is well-ordered, and so is equal to  for
for  the least positive element of
the least positive element of  .
. 
Corollary 2. 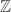 is a PID.
is a PID.
Proof. Any ideal in 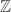 is a well-ordered group, and so must be
is a well-ordered group, and so must be 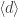 for some
for some  .
. 
Corollary 3. If  is the least solution
is the least solution  to Pell’s equation
to Pell’s equation  , then all solutions are given by
, then all solutions are given by  for
for  .
.
Proof. The solutions  to Pell’s equation form a subgroup of the multiplicative group of units in the ring
to Pell’s equation form a subgroup of the multiplicative group of units in the ring ![\mathbb Z[\sqrt d]](https://s0.wp.com/latex.php?latex=%5Cmathbb+Z%5B%5Csqrt+d%5D&bg=ffffff&fg=333333&s=0&c=20201002) . Since it is well-ordered, the conclusion follows.
. Since it is well-ordered, the conclusion follows. 
We can even improve Proposition 0 a little:
Corollary 4. If  is a subgroup of
is a subgroup of  , then the following are equivalent:
, then the following are equivalent:
(i)  is well-ordered;
is well-ordered;
(ii)  is not dense;
is not dense;
(iii)  is cyclic.
is cyclic.
Proof.  by Proposition 1.
by Proposition 1.  is clear. Suppose that
is clear. Suppose that  is not dense. Then there exist
is not dense. Then there exist  with
with 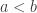 such that
such that  . Then
. Then 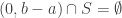 , because
, because  . Therefore
. Therefore 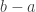 is the minimal element in
is the minimal element in 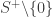 , i.e.
, i.e.  . Thus
. Thus  .
. 
A consequence of Corollary 4 is:
Corollary 5. Let  be a group. If
be a group. If  has a faithful one-dimensional real representation
has a faithful one-dimensional real representation 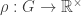 , then
, then  is dense if and only if
is dense if and only if 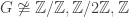 .
.
Note that  is dense if and only if it has two
is dense if and only if it has two 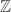 –linearly independent elements; therefore
–linearly independent elements; therefore  must be torsion-free. And since
must be torsion-free. And since 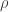 is faithful,
is faithful,  must be abelian:
must be abelian: 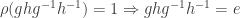 , i.e.
, i.e. 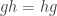 for all
for all 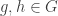 . Thus we get the following nice result:
. Thus we get the following nice result:
Proposition 2. If  has a faithful one-dimensional real representation, then one of the following holds:
has a faithful one-dimensional real representation, then one of the following holds:
(i)  ;
;
(ii)  ;
;
(iii) 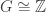 ;
;
(iv)  .
.
Moreover, if  and
and  is finitely generated, then
is finitely generated, then  , for some
, for some  .
.
and
be integers. Consider the ring
.
the greatest common divisor (GCD) of
and
.
is divisible by both
and
.
, called the least common multiple (LCM) of
and
.
and
.
,
and
are subings of
. Moreover,
and
. So by the Chinese Remainder Theorem,
,
,
,
and
. Hence
, i.e.,
.
. As before, we can define
is divisible by
for
.
and
. As before,
,
.
, i.e.
.
by
for any number field
, then
takes the form
.
.
.


